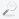 SİTE
İÇİ ARAMA SİTE
İÇİ ARAMA |
|
|
 Blogroll Blogroll |
|
|

|
|
|
|
İkili Ağaçlar (Binary Tree) |
|
| Gönderiliyor lütfen bekleyin... |
|
|
Birçok programcının en az bir defa karşısına çıkan yada çıkma
olasılığı yüksek bir konu olan Binary Tree (İkili Ağaç)’yi
inceleyeceğiz. Ağaç yapısının kullanım alanlarını göz önüne aldığımızda, arama
işlemleri, parsing işlemleri, matematiksel ifadelerin uyarlanması (
örneğin a^3 + b * (c - d) gibi ), sıkıştırma algoritmaları, verilerin
sıralanması, işletim sistemlerindeki dosya sistemi, oyun programlama, veri
tabanı yönetim sitemleri (dbms) ve daha birçok uygulamada sıklıkla
kullanılan bir veri yapısı olduğundan bu konu ile karşılaşma olasılığımızın
neden çok yüksek olduğunu daha iyi anlayabiliriz.
Ağaç veri yapısını incelemeye başladığımızda yukardaki şekilde de
görüldüğü gibi bir çok düğümden (node) oluşmaktadır ve bu
düğümler sonlu sayıdadır(örneğin B, F, K ...). Eğer özel bir ağaç modeli
oluşturmak istenildiğinde herbir düğümün n tane düğümü olabilir. Kök
(root) düğüm (A düğümü) denilen özel bir düğüme sahiptir ve herhangi
bir düğümden yukarı doğru çıkıldığında kök düğüme ulaşılır. Kök düğümün sağ
tarafındaki daldan oluşan ağaca sağ alt ağaç(D, F), sol
tarafındaki daldan oluşan ağaca ise sol alt ağaç(B, C, E, K,
L) denir. Bir düğüme bağlanan sağ ve sol düğümlere alt
(child) düğüm(B’nin alt düğümleri E ve C dir) denir. Bir düğümün bağlı
olduğu düğüme üst (parent) ( K ve L nin
parenti E) düğüm denir. Eğer bir düğümün sağ ve sol alt düğümleri
yoksa bu tür düğümlere yaprak (leaf) düğüm denir. İki düğüm
aynı üst düğüme sahip ise bu iki düğüme kardeş (sibling)
düğüm denir. Ağacımızı oluşturan herhangi bir düğümü incelediğimizde,
öncelikle bu düğümde tutulacak veri kısmı daha sonra sağ ve sol alt düğümler
ile bağlantı oluşturacak göstericilerden oluştuğunu görürüz :
typedef struct testnode {
int data;
struct testnode* p_left_node;
struct testnode* p_right_node;
/* struct testnode* p_x1_node;*/
/* struct testnode* p_x2_node;*/
/* ... */
}test_Node;
Ağaç veri yapısında, düğüm ekleme ,silme, arama, tüm düğümleri
silme, kök düğümü oluşturma ve ağaç düğümlerini dolaşma işlemlerini
gerçekleştirebiliriz. Bu işlemleri ikili ağaç veri yapısı üzerinde
gerçekleştirelim. İkili ağaç veri yapısında herbir düğümün en fazla 2 adet alt
düğümü olabilir. Tabi unutmamamak gerekir ki bir düğüm hiçbir alt düğüme
sahip olmayabilir. Aslında ikili ağaçlar daha önceden incelediğimiz bağlı
listelerin özel biçimi de diyebiliriz. İkili ağaçların önemli özelliği eğer
sıralanırsa çok hızlı bir şekilde ekleme, silme arama işlemlerini
yapabilabilmesidir. Ağaç veri yapısı üzerinde işlem yapan fonksiyonların
birçoğu kendi kendini çağıran (recursive) fonksiyonlardır. Çünkü bir ağacı alt
ağaçlara böldüğümüzde elde edilen her parça yine bir ağaç olacaktır ve
fonksiyonumuz yine bu ağaç üzerinde işlem yapacağı için kendi kendini
çağıracaktır. İkili ağaç yapısının önemli bir özelliği de düğümlerin
yerleştirilmesi sırasında uygulanan işlemlerdir. İkli ağaçlarda kök hücresinden
başlayarak, eğer eklenecek düğümün veri kısmındaki değer, kök düğümünün
veri kısmındaki değerden büyük ise sağ tarafa , küçük yada eşit ise sol tarafa
eklenir.Bu şekilde olşturulan sıralı ikili ağaçta biliriz ki , sol alt ağaçtaki
düğümlerde kökten küçük ya da köke eşit değerler, sağ alt ağaçtaki düğümlerde
ise kökten büyük değerler bulunur.
Yukardaki şekildeki gibi bir sıralı ikili ağacımızın olduğunu
düşünelim. Bu ağaç üzerinde arama işlemlerini adım adım inceleyelim :
1- Örnğin ağaçta 40 değerini arayalım.
Adım 1 : 40 ile 60 karşılaştırılır. 40 < 60 olduğundan
sola doğru dallanılır.
Adım 2 : 40 ile 38 karşılaştırılır. 40 > 38 olduğundan sağa doğru
dallanılır.
Adım 3 : 40 ile 43 karşılaştırılır. 40 < 43 olduğundan sola doğru
dallanılır.
Adım 4 : 43 ile 43 karşılaştırılır. 43 = 43 olduğundan arama işlemi bitmiştir.
2- Örneğin ağaçta 62 değerini arayalım.
Adım 1 : 62 ile 60 karşılaştırılır. 62 > 60 olduğundan sağa doğru
dallanılır.
Adım 2 : 62 ile 78 karşılaştırılır. 62 < 78 olduğunda sola doğru
dallanılır.
Adım 3 : 62 ile 65 karşılaştırılır. 62 < 65 olduğundan sola doğru
dallanılır.
Adım 4 : NULL değer elde edildiği için arama işlemi sona erdirilmiştir.Aranan
değer bulunamamıştır.
Ağaç yapısı üzerinde herhangi bir düğüme erişme sürecimize ağacı
gezmek (traverse) denir. Bir ağacı ençok bilinen üç değişik yöntemle
gezebiliriz :
1- Sıralı (inorder) : İlk
adımda sol alt ağaç sıralı şekilde dolaşılır (a-b-c). Kök düğüme uğranır
(d). Son adımda sağ alt ağaç sıralı şekilde dolaşılır (e-f-g). Sonuçta ağaç
sırasıyla a-b-c-d-e-f-g düğümlerine erişilerek gezilir.
2- Kökten Başlayarak (preorder) : İlk adımda köke uğranır(d).
Sol alt ağaç kökten başlayarak dolaşılır (b-a-c). Son adımda sol alt ağaç
kökten başlayarak dolaşılır (f-e-g). Sonuçta ağaç sırasıyla d-b-a-c-f-e-g
düğümlerine erişilerek gezilir.
3-Sondan Başlayarak (postorder) : İlk adımda sol alt ağaç
sondan başlayarak dolaşılır (a-c-b). İkinci adımda sağ alt ağaç sondan
başlayarak dolaşılır (e-g-f). Son adımda ise köke uğranır(d). Sonuçta
ağaç sırasıyla a-c-b-e-g-f-d düğümlerine erişilerek gezilir.
Yapacağımız uygulamalarda ağacın sıralı olmasını istemeyebiliriz. Buna karşın
birçok uygulamada ağacın sıralı olması gerekliliği ile karşılaşırız. Tabiki bir
ağacın sıralı yada sırasız olması ağacın dolaşım şekline göre belirlenir.
Sıklıkla kullanılan ağaç şekli sıralı ağaç olduğunda bizde örneklerimizi sıralı
ağaç veri yapısı üzerinde gerçekleştireceğiz. Bu nedenle ağacı yapılandırırken,
sol alt ağacın kökten küçük veya eşit değerler içerdiğini, sağ alt ağacın ise
kökten büyük değerler içerdiğini göz önünde bulundurmalıyız. Şimdi işlemleri
gerçekleştirecek fonksiyonlarımızı yazmaya başlayalım. İlk olarak ağacımızı
oluşturacak fonksiyonumuzu yazalım.
typedef struct _tree {
int data;
struct _tree* p_left;
struct _tree* p_right;
}Tree, *HTree;
HTree CreateTree(HTree root, HTree node, int data);
HTree g_root = NULL;
HTree CreateTree(HTree root, HTree node, int data) {
if (!node) {
node = (HTree) malloc(sizeof
(Tree));
if (!node) {
puts("Yeterli bellek yok!\n program sonlandiriliyor..");
exit(EXIT_FAILURE);
}
node->p_left = NULL;
node->p_right = NULL;
node->data = data;
if (!root) /* ilk
kayıt ise */
return node;
if (data < root->data)
root->p_left = node;
else
root->p_right
= node;
return node;
}
if (data < node->data)
CreateTree(node, node->p_left,
data);
else
CreateTree(node, node->p_right,
data);
return root;
}
|
İlk adımda typedef anahtar kelimesini kullanarak
ağaçtaki herbir düğümü temsil edecek yapıyı oluşturduk. Tree struct _ tree
türünden bir nesneyi, HTree ise bu yapı türünden bir göstericiyi temsil
etmektedir. g_root, ağacın kökünü tutacak global bir değişkendir. CreateTree
fonksiyonu ise ağacımızı oluşturan fonksiyondur. Fonksiyonun ilk parametresi
ağacın kökünü gösteren bir gösterici , ikinci parametresi ise ağaçta aranacak
düğümü, son parametresi ise düğümün veri kısmında saklanacak değeri
göstermektedir. Fonksiyon yeni bir kayıt ekleneceği zaman düğümün veri
kısmındaki değeri dikkate alarak doğru kaydı buluncaya kadar sol yada sağ
tarafa giderek düğümler arasındaki bağlantıları izlemektedir. Bağlı
listelerdeki gibi burda da ağacın kökünü tutacak struct _tree yapısı türünde
global bir göstericiye ihtiyacımız var. CreateTree fonksiyonunu ilk defa
kullandığımızda bize ağacın kökünü gösteren bir gösterici ile geri dönecektir.
Bu noktada g_root göstericisine bu değeri atamalıyız. Bu fonksiyonu ilk defa
şöyle kullanmalıyız :
rootTree = CreateTree(rootTree, rootTree, data);
Bunun nedeni ağacımızda henüz hiçbir düğüm mevcut değildir.Hem ağacın
kökü belirlemek hem de ağaca ilk düğümü eklemek istediğimizden bu şekilde
kullanım şarttır. Daha sonraki fonksiyon çağrımlarında yine kökü gösteren
göstericiyi geri dönüş parametresi olarak elde edebiliriz. Şimdi daha önce
tanımlamalarını yaptığımız, ağacı gezen fonksiyonları yazalım.
void InorderTraverse(HTree root) /*
Sıralı dolaşma */
{
if (!root) return;
InorderTraverse(root->p_left);
if (root->data)
printf("%d ", root->data);
InorderTraverse(root->p_right);
}
void PreorderTraverse(HTree root) /* Kökten başlayarak */
{
if (!root) return;
if (root->data)
printf("%d ", root->data);
PreorderTraverse(root->p_left);
PreorderTraverse(root->p_right);
}
void PostorderTraverse(HTree root) /* Sondan başlayarak */
{
if (!root) return;
PostorderTraverse(root->p_left);
PostorderTraverse(root->p_right);
if (root->data)
printf("%d ", root->data);
} |
Görüldüğü gibi fonksiyonlar ağacı üç parçaya ayrılmış gibi
dolaşmaktadır. Sağ alt ağaç, sol alt ağaç ve kök. Tanımlamalarda yaptığımız
gibi sıralı dolaşmada (InorderTraverse) önce sol alt ağaç, sonra kök,
sonra sağ alt ağaç, kökten başlayarak dolaşmada (PreorderTraverse) önce
kök, sonra sol alt ağaç, son adımda ise sağ alt ağaç, sondan başlayarak
dolaşmada (PostorderTraverse) ise, önce sol alt ağaç, sonra sağ alt ağaç son
adımda ise köke uğranılarak ağacı dolaşma işlemi gerçekleştirilir.
Ağaç üzerinde arama işlemi oldukça basit olmasına karşın çok hızlıdır. Kendi
kendi çağıran bir fonksiyon değildir arama fonksiyonu. Aranacak değeri kökün
değeri ile karşılaştırırız. Eğer küçük ise sol tarafa, büyük ise sağ tarafa
doğru dallanarak arama işlemine devam ederiz.
HTree SearchTree(HTree root, int data)
{
if(!root) /* Eğer ağaç boş ise */
return root;
while(root->data != data) {
if (data < root->data)
root =
root->p_left;
else
root =
root->p_right;
if (root == NULL)
break;
}
return root;
}
|
Birçok algoritmanın geliştirilmesinde, büyük problemleri çözümünde
önemli ölçüde fayda sağlayan özellikle de arama uygulamalarında vazgeçilmez bir
yöntem olan ikili ağaçlar konusuna değindik. İyi tasarlanmış bir ikili ağaç ile
diğer arama tekniklerinden çok daha hızlı bir arama işlemi
gerçekleştirilebilir.
Uygulamanın kaynak kodlarını ve
çalıştırılabilir dosyasını buradan indirebilirsiniz.
Mutlu ve sağlıklı günler.
Makale:
İkili Ağaçlar (Binary Tree) C ve Sistem Programlama Oğuz Yağmur
|
|
|
|
|
-
-
Eklenen Son 10
-
Bu Konuda Geçmiş 10
Bu Konuda Yazılmış Yazılmış 10 Makale Yükleniyor
Son Eklenen 10 Makale Yükleniyor
Bu Konuda Yazılmış Geçmiş Makaleler Yükleniyor
|
|
|
|